A multicyclic polymer chain can form novel multicyclic polymer molecular structures depending on the number of rings, the number of linear side branches and the junction points. In this study, we investigated the effect of polymer molecular structure on the change in polymer properties using lasso and manacle polymers of the same molecular weight, consisting of a ring and a linear side branch. To investigate the ideal behaviour of the polymer chains, we adopted a freely jointed bead-rod model in a free-draining solution system and performed a mesoscopic Brownian dynamics simulation. Despite having the same molecular weight, linear, ring (or cyclic), lasso-shaped and manacle-shaped polymer chains exhibit different physical and dynamic properties in equilibrium and nonequilibrium (or shear flow) states. In particular, lasso-shaped and manacle-shaped polymer chains, which differ in the number and size of the rings and their position in the chain, exhibit completely different physical properties and tumbling behaviour depending on their molecular architecture.

멀티 고리형 고분자 체인(multicyclic polymer chain)은 고리(ring)의 개수, 선형 곁가지(linear side branch) 개수, 분기점(junction point)에 따라 새로운 멀티 고리형 고분자 분자 구조를 만들어 낼 수 있다. 본 연구에서는 하나의 고리와 하나의 선형 곁가지로 이루어진 동일한 분자량의 올가미형 고분자(lasso polymer)와 수갑형 고분자(manacle polymer)를 이용하여 고분자 분자 구조가 고분자의 특성 변화에 미치는 영향을 조사하였다. 고분자 체인의 이상적인 거동을 살펴보기 위해 자유 배수 용액(free-draining solution system)하 랜덤하게 연결된 비드-로드 모델(freely jointed bead-rod model)을 채용하여 중시 기반 브라운 동역학 전산 모사를 진행하였다. 선형, 고리형, 올가미형, 수갑형 고분자 체인들은 동일한 분자량을 가짐에도 불구하고 평형 및 비평형(또는 전단 유동) 상태에서 상이한 물리적, 동역학적 성질을 보여주었다. 특히, 고리의 개수와 크기 및 체인 내의 위치가 다른 올가미형 고분자 체인과 수갑형 고분자 체인은 분자 구조에 따라 완전히 다른 물리적 특성 및 텀블링 거동을 확인할 수 있었다.

The effect of polymer molecular structure on the change in polymer properties was investigated using multicyclic polymer of the same molecular weight. To investigate the ideal behaviour of the polymer chains, we adopted a freely jointed bead-rod model in a free-draining solution system and performed a mesoscopic Brownian dynamics simulation. Despite having the same molecular weight, linear, ring (or cyclic), lasso-shaped and manacle-shaped polymer chains exhibit different physical and dynamic properties in equilibrium and nonequilibrium states. In particular, the polymer chains exhibited different chain tumbling and rotation mechanisms at high shear flow strength as shown below.

Keywords: multicyclic polymer, brownian dynamics, shear flow, free-draining system.

본 연구는 2025년 경기대학교 대학원 연구원장학생 장학금 지원에 의하여 수행되었음.

저자들은 이해상충이 없음을 선언합니다.

최근 고분자 합성 기술의 눈부신 발전으로 인해 다양한 분자 구조(molecular architecture)를 가지는 고분자 물질들이 합성되고 있다.^1-8 새롭게 합성된 고분자 물질들은 기존 고분자 물질과는 상이한 구조적, 물리적, 열역학적, 동역학적 특성을 보여주어 기존 소재 대체 및 신소재 개발에 있어 새로운 대안으로 떠오르고 있다.^9-26 예를 들어, 선형 고분자(linear polymer)의 끝을 연결하여 합성한 고리형 고분자(ring or cyclic polymer)는 동일한 분자량을 가지는 선형 고분자에 비해 매우 다른 물리적, 동역학적, 유변학적 특성을 보여준다.^9-23 고리형 고분자는 동일한 분자량을 가지는 선형 고분자에 비해 빠른 확산, 빠른 이완 시간, 낮은 점도, 높은 유리 전이 온도 등을 보여 준다. 이러한 고리형 고분자의 특징들은 약물 전달 시스템을 개선하거나 새로운 고분자 재료 개발에 매우 유용하게 활용될 것이라 예상된다.^27,28
고리형 고분자는 선형 고분자의 특징인 자유 말단(free chain end)이 없는 폐쇄 루프 구조(closed-loop structure)를 가지고 있기 때문에 기존 고분자 이론 및 모델을 이용하여 그 거동을 설명할 수 없다. 따라서, 이러한 고리형 고분자의 독특한 거동을 설명하기 위해 현재 많은 연구가 활발히 이루어지고 있다.^9-23 특히, 고리형 고분자 합성 과정 중, 선형 고분자를 고리형 고분자로부터 분리 및 정제하는 과정은 실험적으로 쉽지 않다.^4-9 따라서, 이러한 정제 과정의 어려움을 극복하기 위해 컴퓨터 전산 모사(computer simulation)를 이용한 고리형 고분자 연구가 새로운 대안으로 떠오르고 있다.
최근에는 고리형 고분자에 대한 이해를 바탕으로 더욱 복잡한 멀티고리형 고분자(multi cyclic polymer)에 대한 연구로 확장되고 있다.^29-42 복잡한 구조를 지닌 멀티 고리형 고분자 시스템들은 체인 내 고리(ring)의 개수, 선형 곁가지(linear side branch)의 개수, 분기점(branch point)의 배치에 따라 크게 ‘fused’, ‘spiro’, ‘bridged’ 형태로 분류되게 된다.⁴ Fused 형태의 대표적인 고분자 체인은 올가미형 또는 올챙이형 고분자 체인이고(lasso or tadpole polymer chain), spiro 형태의 대표적인 고분자 체인은 8자 모양 고분자 체인(8-shaped polymer chain)이며, bridged 형태의 대표적인 고분자 체인은 수갑형 고분자 체인(manacle polymer chain)을 들 수 있다. 본 연구에서는 이러한 멀티 고리형 고분자 체인의 분자 구조에 따른 고분자 시스템의 물리적, 동역학적, 유변학적 특성을 체계적으로 분석하기 위해 두 가지 형태의 멀티 고리형 고분자 체인을 고안하였고 이에 상응하는 순수 선형 고분자 체인 및 고리형 고분자 체인과 비교 및 분석을 실시하였다. 두 가지 형태의 멀티 고리형 고분자 체인(올가미형 고분자 체인과 수갑형 고분자 체인)들은 동일한 분자량을 가지고 있을 뿐만 아니라 고분자 체인을 구성하고 있는 선형 부분과 고리형 부분 역시 같은 분자량을 가지고 있게 디자인하였다.
선형, 고리형, 올가미형, 수갑형 고분자 체인 시스템의 거동을 조사하기 위해 비드-로드 모델(bead-rod model)을 이용한 중시 기반 브라운 동역학 전산 모사(mesoscopic Brownian dynamics simulation) 방법을 채택하였다. 이상적인 고분자 체인의 거동을 살펴보기 위해 유체역학적 상호작용(hydrodynamic interactions)을 배제한 자유 배수 용액 시스템(free-draining solution system) 하에서 평형 상태 및 비평형 상태(equilibrium and non-equilibrium state)의 고립된 단일 체인(isolated single chain)을 관찰하였다. 일반적으로 고분자의 구조적, 동역학적, 유변학적 특성들은 분자량에 영향을 많이 받는데 반하여 동일한 분자량을 가지는 선형, 고리형, 올가미형, 수갑형 고분자 체인 시스템은 분자 구조에 따라 각기 다른 물리적, 동역학적, 유변학적 특성을 보여주었다. 특히, 동일한 분자량을 가지고 있지만 고리형 부분의 개수와 체인 내에서 배치가 다른 올가미형 고분자 체인과 수갑형 고분자 체인은 완전히 다른 거동을 보여주었다.

전산 모사 방법. 본 연구에서는 고분자 사슬의 특성을 조사하기 위해 광범위한 중시 기반 브라운 동역학 전산 모사(mesoscopic Brownian dynamics simulation)를 진행하였다. 특히, 이상적인 고분자 사슬들의 거동을 살펴보기 위해 분자 간 또는 분자 내 상호 작용(intra- or inter-molecular interactions)을 배제시킨 자유 배수 용액 시스템(free-draining solution system) 하의 고립된 단일 고분자 체인(isolated single polymer chain)의 거동을 조사하였다. 참고로 자유 배수 용액 하 고립된 단일 고분자 체인의 거동은 고분자 용융체(polymer melts) 또는 고농축 고분자 용액(concentrated polymer solutions)에서의 고분자 체인의 거동과 잘 일치한다고 알려져 있다.⁴³ 자유 배수 용액 시스템 하 고분자 체인의 거동을 묘사하기 위해 본 연구에서는 멀티 비드-로드 (multi bead-rod) 모델을 사용하였다. 중시 기반 브라운 동역학 전산 모사에서 자유롭게 연결된 각각의 비드(freely jointed beads)에는 세 가지 외부 힘(external forces)이 작용한다. 각각의 비드에 작용하는 힘에 대한 수지 식(force balance equation)으로부터 시간에 따른 각각의 비드의 위치를 계산할 수 있다. 본 연구에서는 위치 벡터(position vector)를 이용하여 각각의 비드의 위치를 나타냈다. 시간에 따른 비드의 위치 벡터에 대한 진화 방정식(evolution equation for the bead position vector)은 비드에 작용하는 힘에 대한 수지식으로부터 유도하여 식 (1)과 같이 확률 미분 방정식(stochastic differential equation, SDE) 형태로 나타낼 수 있다.⁴³ 각각의 비드에 대한 위치 벡터의 SDE를 Liu의 반복 방법(iterative method)을 통해 수치적으로 적분하면 시간에 따른 위치 벡터를 계산할 수 있게 되고 궁극적으로 시간에 따른 비드의 거동 및 고분자 체인의 거동을 묘사할 수 있게 된다.⁴⁴



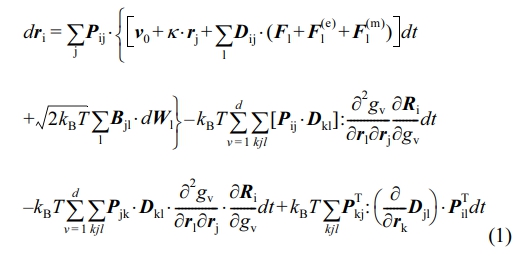
이 때 r_i는 비드 i의 위치 벡터(position vector)를 나타내고, P_ij는 동적 투영 텐서(dynamical projection tensor)를 의미한다. 또한 F_i, F^(e)_i, F⁽ⁿ⁾_i 은 각각 비드에 작용하는 내부 힘(internal force), 임의의 비드에 작용하는 외력(external force), 그리고 임의의 비드에 작용하는 메트릭 힘(metric force)을 의미한다. 또한 D_ij는 모빌리티 텐서(mobility tensor)이고 B_ij는 모빌리티 텐서의 분해 텐서(decomposed tensor)이며 이는 D_ij = Σ_kB_ik·B^T_jk 의 관계를 가진다. k_B는 볼츠만 상수(Boltzmann constant)이고 g_v는 제약 조건(constraint)이며 k 는 속도 구배 텐서(velocity gradient tensor)이다.

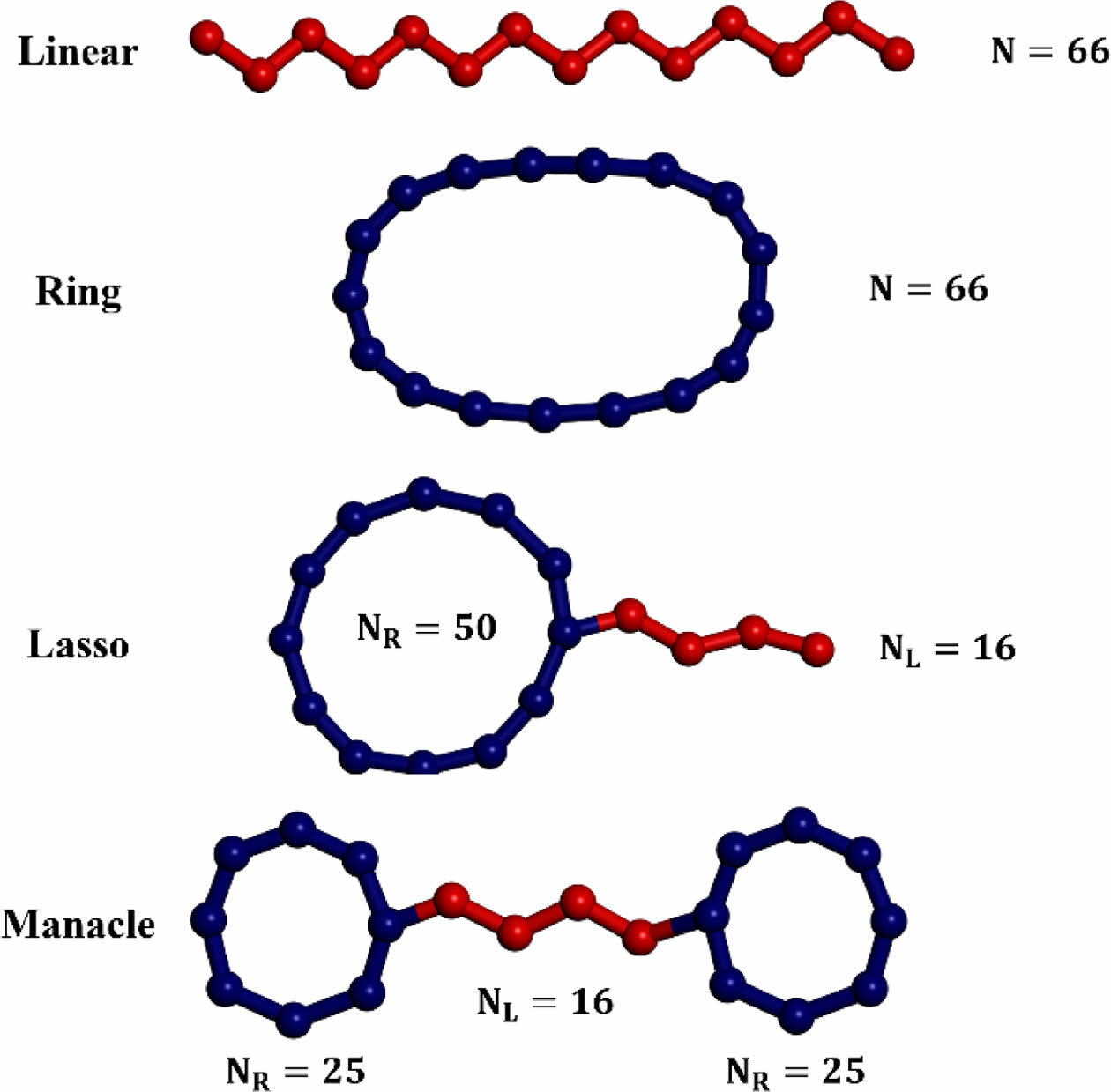
고분자 사슬 시스템. 고분자 체인의 분자 구조에 따라 나타나는 물리적, 동역학적 특성을 체계적으로 조사하기 위해 네 가지 종류의 고분자 체인을 비교하였다. 각 고분자 체인들은 체인당 동일한 분자량 또는 동일한 비드 수(same molecular weight or same number of beads)를 가지지만 그 분자 구조는 서로 상이하다. Figure 1에서 보듯이 각 고분자 체인 시스템은 총 66개의 비드로 구성되어 있다. 선형 고분자 체인(linear polymer chain, L66)과 고리형 고분자 체인(ring or cyclic polymer chain, R66) 체인은 곁가지를 포함하지 않는 순수한 기본 고분자 체인 형태이다. 올가미형 또는 올챙이형 고분자 체인(lasso or tadpole-shaped polymer chain)의 경우 50개 비드로 구성된 고리형 부분(ring part)과 16개의 비드로 이루어진 선형 곁가지(linear side branch)가 합쳐진 구조이다. 수갑형 고분자 체인(manacle polymer chain)은 양쪽 끝에 25개의 비드로 구성된 고리형 부분(ring part)이 16개의 비드로 이루어진 선형 브릿지 부분(linear bridge part)에 의해 연결되어 있는 구조이다. 선형 부분과 고리형 부분의 조합으로 이루어진 올가미형 고분자 체인과 수갑형 고분자 체인은 선형 고분자 체인의 구조적 특징인 자유 말단(free chain end)과 고리형 고분자 체인의 구조적 특징인 폐쇄 루프 구조(closed-loop structure)를 동시에 가지고 있어 매우 다양한 물리적, 동역학적 특성을 보여줄 것으로 예상된다. 전단 유동 하 선형 폴리에틸렌 체인에 대한 분자 동역학 및 브라운 동역학 전산 모사 결과로부터 하나의 비드는 여섯 개의 CH₂에 해당한다는 사실이 알려져 있다.⁴⁵ 따라서, 비드-로드 모델을 이용한 각 고분자 체인 시스템의 총 분자량은 C₃₉₆H₇₉₄의 분자량과 같고, 올가미형 고분자 체인의 고리형 부분은 C₃₀₀H₆₀₀, 선형 곁가지 부분은 C₉₆H₁₉₄에 해당하며, 수갑형 고분자 체인의 각 고리형 부분은 C₁₅₀H₃₀₀, 선형 브릿지 부분은 C₉₆H₁₉₄에 해당한다.
본 연구에서 전단 유동의 세기는 전단율(shear rate)과 완화 시간(relaxation time)의 곱인 Weissenberg number (Wi)로 나타냈었으며, 선형 점탄성 영역(linear viscoelastic regime)에서부터 비선형 점탄성 영역(nonlinear viscoelastic regime)까지 광범위한 영역에 걸쳐 체계적인 전산 모사를 진행하였다.

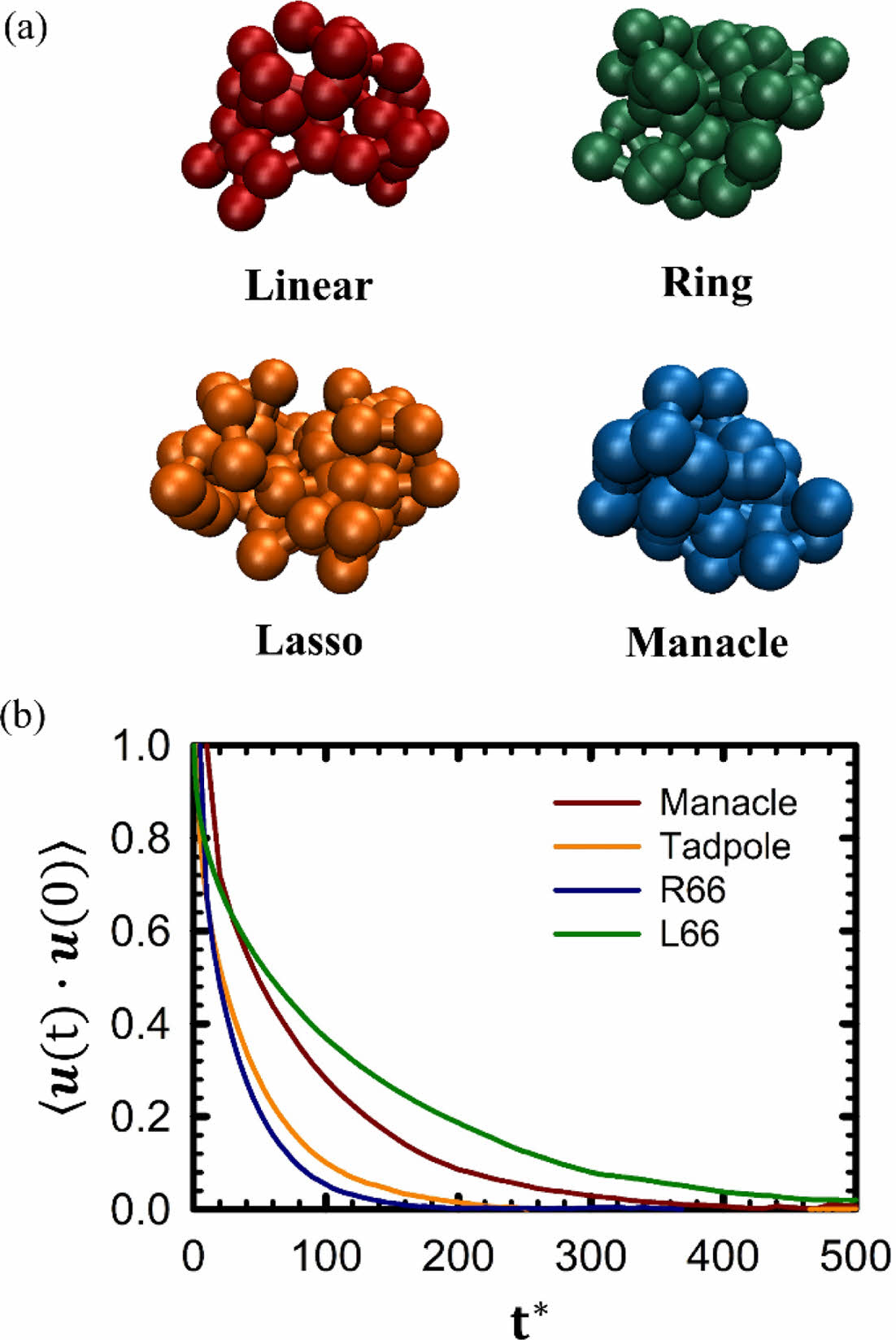
평형상태(Equilibrium State). 고분자 이론 및 모델에 따르면 평형상태(equilibrium state)에서 가우시안 분포(Gaussian distribution)를 따르는 고분자 사슬들은 전체적으로 랜덤하게 코일된 체인 형태(randomly coiled chain conformation)를 보여준다.^9,10 이러한 평형상태의 고분자 체인 형태를 관찰하기 위해 각 고분자 체인 시스템에서 무작위로 한 개의 고분자 체인을 선택하여 Figure 2(a)에 나타내었다. Figure 2(a)에서 볼 수 있듯이, 무작위로 선택된 각 고분자 체인은 고분자 분자 구조와 상관없이 랜덤하게 코일된 체인 형태를 띄고 있다. 각 고분자 체인의 이러한 특정적인 형태는 선행 고분자 이론 및 모델, 고분자 실험, 고분자 전산 모사 결과와 잘 일치한다.^9-23
일반적으로 랜덤하게 코일된 형태를 지닌 고분자 체인의 크기는 고분자 체인의 분자량에 따라 증가한다.^9,10 그러나, 고분자 동역학 모델 중 하나인 Ring-Rouse 모델에 따르면, 동일한 분자량을 가지는 선형 및 고리형 고분자 체인을 비교할 때, 이론적으로 고리형 고분자 체인의 크기가 선형 고분자 체인보다 더 작다고 한다.^16,17 이를 확인하기 위해 평형상태에서 각 고분자 체인 시스템의 크기를 비교하였다. 먼저, 고분자 체인의 크기를 비교 하기 위해 각 고분자 체인의 평균 제곱 체인 종단 거리(mean-square chain end-to-end distance, (R²_ete)와 평균 제곱 고리 지름(mean-sqaure chain ring diameter, (R²_g)을 계산하였다.
특히, 고리형 고분자 체인의 경우 양쪽 체인 끝이 없는 폐쇄 루프 구조(closed-loop structure)를 가지고 있기 때문에 평균 체인 종단 거리 대신 고리의 지름을 평균한 평균 제곱 고리 지름(mean-square chain ring diameter, (R²_d)을 사용하였다. 계산 결과 선형 고분자 체인(L66)은 (R²_ete)= 65.86, (R²_g)=11.01, 고리형 고분자 체인(R66)은 (R²_d)=16.79, (R²_g)=5.59, 수갑형 고분자 체인은 (R²_ete)=25.24, (R²_g)=6.39 이고, 올챙이형 고분자 체인은 (R²_ete)=24.67, (R²_g)=5.51 였다. 예상과는 달리, 각 고분자 체인 시스템은 같은 분자량 또는 같은 비드 수를 가지고 있었지만 분자 구조에 따라 고분자 체인의 크기가 많이 다름을 보여주었다. 평형상태에서 같은 분자량 또는 같은 비드 수를 가지는 고분자 체인의 크기는 고리형 고분자 체인(R66) < 올가미형 고분자 체인 < 수갑형 고분자 체인 < 선형 고분자 체인(L66) 순으로 증가하였다. Ring-Rouse 모델에 따르면 같은 분자량을 가지는 선형 및 고리형 고분자 체인은 이론적으로 (R²_g)_L/(R²_g)_R=2의 관계식을 만족한다고 한다.^16,17 자유 배수 용액 시스템에서 순수 선형 고분자 체인(L66)과 순수 고리형 체인(R66)은 (R²_g)_L66/(R²_g)_R66=1.99 값을 보여주기 때문에 이러한 Ring-Rouse 모델과 잘 일치함을 확인할 수 있다.

고분자 이론 및 모델에 따르면 랜덤하게 코일된 형태를 지닌 고분자 체인은 이론적으로 (R²_ete)_L/(R²_g)_R=6 값을 가진다.^9,10 각 고분자 체인 시스템에 대하여 (R²_ete)/(R²_g)을 계산해 보면 선형 고분자 사슬은 (R²_ete)/(R²_g)=5.98, 고리형 고분자 사슬은 (R²_ete)/(R²_g)=3.00, 수갑형 고분자 사슬은 (R²_ete)/(R²_g)=3.95, 올가미형 고분자 사슬은 (R²_ete)/(R²_g)=4.48 보여 주었다. 결과적으로, 선형 및 고리형 고분자 체인은 랜덤하게 코일된 형태를 지닌 고분자 체인의 이론 값과 잘 일치함을 보여주었고 올가미형 고분자 체인과 수갑형 고분자 체인은 랜덤하게 코일된 형태를 보여주고 있음에도 불구하고 이론 값에서 벗어나는 결과를 보여주었다.

고분자 체인 시스템에 있어서 가장 긴 회전 완화 시간(longest rotational relaxation time) 또는 Rouse 시간(Rouse time)은 고분자 체인 시스템의 동적 특성을 가장 잘 나타내는 속성 중에 하나이다. 일반적으로 고분자 체인의 가장 긴 완화 시간은 분자량의 제곱에 비례하게 증가하는 것으로 알려져 있다.^9,10 또한, 최근 연구에 따르면 고리형 고분자 체인의 경우 같은 분자량을 가지는 선형 고분자 체인보다 더 빠른 완화 시간을 갖는다고 알려져 있다.^20,21 Figure 2(b)는 각 고분자 체인 시스템의 체인 종단 간 단위 벡터(chain unit end-to-end vector, u)의 시간 상관 관계 함수(time correlation function, TCF)를 상관 시간(correlation time)에 따른 함수로 나타냈다. 고분자 이론 및 모델에 따르면, 가장 긴 회전 완화 시간은 체인 종단 간 단위 벡터의 시간 상관 관계 함수를 지수 붕괴 함수(exponential decay function)에 회귀시켜 얻을 수 있다. 각 고분자 체인 시스템에 대해 가장 긴 완화 시간을 계산해 보면, 선형 고분자 체인(L66)은 109. 41, 고리형 고분자 체인(R66)은 29.92, 올가미형 고분자 체인은 44.41, 수갑형 고분자 체인은 77.48이었다. 같은 분자량을 가지는 고분자 체인 시스템에서 가장 긴 완화 시간(relaxation time, t)은 분자 구조에 따라 고리형 고분자(R66) < 올가미형 고분자 < 수갑형 고분자 < 선형 고분자(L66) 순으로 증가한다. Ring-Rouse 모델에 따르면 랜덤하게 코일된 형태를 가지는 선형 및 고리형 고분자 체인은 이론적으로 τ_R,Linear/τ_R,Ring=4 관계를 가진다.^16,17 자유 배수 용액 하 선형 고분자 체인(L66)과 고리형 고분자 체인(R66)에 대해 이를 계산해 보면 τ_R,L66/τ_R,R66=3.66으로 이론 값과 비슷한 값을 보여준다.
앞서 살펴보았듯이, 평형상태에서 같은 분자량을 가지는 고분자들의 정적 및 동역학적 특성(static and dynamic properties)이 고분자 체인의 분자 구조에 따라 달라짐을 확인할 수 있다.
비평형상태(Non-equilibrium State). 분자 구조가 각 고분자 체인의 유변학적 형태 및 거동에 미치는 영향을 조사 및 분석하기 위해 전단 흐름(shear flow)을 이용하여 각 고분자 체인의 구조적, 동역학적, 유변학적 특성을 조사하였다.
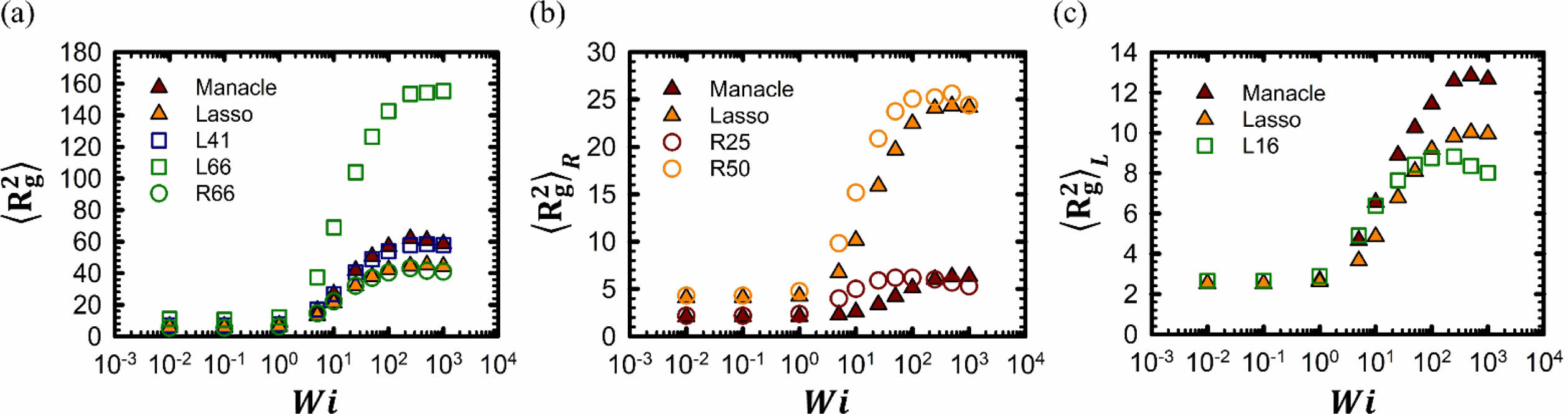
먼저, 고분자 체인의 유체역학적인 형태 변화에 따른 구조적 특성을 파악하기 위해 전단 유동 세기에 따른 평균 제곱 체인 회전 반경(mean-square chain radius of gyration, (R²_g)을 조사하였다. Figure 3(a)에 나타냈듯이, 자유 배수 용액 하 각 고분자 체인 시스템은 전단 유동의 세기에 따라 고분자 용액 속 고분자 체인과 같은 일반적인 유변학적 거동을 보여주었다.⁴⁵ 낮은 전단 유동 세기 영역(Wi < 1)에서 각 고분자 체인 시스템은 일정한 (R²_g) 값을 유지하였다. 고분자 체인 스트레칭과 흐름 방향 정렬(polymer chain stretching and alignment to flow direction)로 인해 중간 전단 유동 세기 영역(1 < Wi < 100)에서 각 고분자 체인 시스템의 (R²_g) 값은 급격히 증가하는 모습을 보여준다. 유동 세기가 매우 강한 높은 전단 유동 영역(Wi > 100)에서는 고분자 체인의 회전 및 텀블링 거동 때문에 각 고분자 체인 시스템의 (R²_g) 값은 더 이상 증가하지 않고 정체 영역(plateau regime)으로 수렴하거나 오히려 감소하게 된다.
최신 고분자 동역학 모델 중 하나인 Ring-Rouse 모델에 따르면 선형고분자 체인과 고리형 고분자 체인은 이론적으로 (R²_ete)/(R²_d)=2 관계를 따른다.^16,17 따라서 각각 50개, 25개의 비드를 가지고 있는 올가미형 또는 수갑형 고분자 체인의 고리형 부분은 각각 25개, 12.5개의 비드를 가지는 선형 고분자에 상응한다. 이를 바탕으로 올가미형 또는 수갑형 고분자 체인 길이에 상응하는 선형 고분자 체인 길이를 계산하면 41개 비드를 가지는 고분자 체인(L41)이 된다. Figure 3(a)에서 보듯이 같은 전단 유동 세기에서 수갑형 고분자 체인은 선형 고분자 체인 L41과 매우 비슷한 (R²_g) 값을 가진다. 따라서 수갑형 고분자 체인은 선형 고분자 체인과 비슷한 유변학적 형태 및 특성을 가질 것으로 예측된다. 하지만, 올가미형 고분자 체인의 경우 선형 고분자 체인 L41과 비교하여 매우 다른 값을 보여주며 오히려 순수 고리형 고분자(R66)와 비슷한 값을 보여준다. 따라서, 고리형 부분이 큰 비율을 차지하는 올가미형 고분자는 순수 고리형 고분자와 유변학적 형태와 특성이 비슷할 것으로 예상할 수 있다.
같은 전단 유동 세기에서 각 고분자 체인 시스템의 (R²_g) 값을 비교해 보면 그 크기는 고리형 고분자(R66) < 올가미형 고분자 < 수갑형 고분자 < 선형 고분자(L66) 순으로 증가한다. 이러한 전단 유동 하 각 고분자 체인의 크기 차이를 좀 더 면밀히 살펴보기 위해 각 고분자 체인을 고리형 부분과 선형 부분으로 나눠 각각의 (R²_g) 값을 조사해 보았다. 특히, 각 고리형 및 선형 부분에 상응하는 순수 고분자 체인과의 비교를 통해 올가미형 고분자 체인 및 수갑형 고분자 체인에서 어느 부분이 많이 변형되는지 자세히 관찰해 보았다.
Figure 3(b)에서 볼 수 있듯이, 올가미형 고분자 체인과 수갑형 고분자 체인의 고리형 부분은 전단 유동 세기에 따라 각각 상응하는 순수 고리형 고분자 체인 R50과 R25와 전반적으로 비슷한 증가 경향을 보여준다. 하지만, 올가미형 고분자 체인과 수갑형 고분자 체인의 고리형 부분은 모두 중간 전단 유동 세기 영역에서 각각 상응하는 순수 고리형 고분자 체인보다 같은 전단 유동 세기에서 약간 낮은 값을 보여준다. 이는 각 고분자 체인 시스템에서 고리형 부분이 같은 전단 유동 세기에 대해 순수 고리형 고분자 보다 덜 스트레칭되고 약간 뭉쳐 있다는 것을 의미한다. 높은 전단 유동 세기 영역에서 고리형 부분은 일정한 (R²_g) 유지하는 대신에 순수 고리형 체인은 약간 감소하는 경향을 보여준다. 이는 순수 고리형 체인과 고분자 체인에 부착된 고리형 부분의 회전 및 텀블링 메커니즘의 차이라고 여겨진다. 순수 고리형 체인 같은 경우는 완전한 체인 회전 및 텀블링을 보여주지만, 한쪽 끝이 선형 부분에 연결된 고리형 부분은 완전한 체인 회전 및 텀블링이 가능하지 않으리라 생각된다.
Figure 3(c)에서 보듯이, 각 고분자 체인의 선형 부분은 낮은 전단 유동 세기에서부터 중간 전단 유동 세기까지 상응하는 선형 고분자 체인(L16)과 거의 비슷한 증가 경향 및 값을 보여준다. 하지만, 높은 전단 유동 세기에서 각 고분자 체인의 선형 부분은 상응하는 선형 고분자 체인(L16)보다 높은 값을 가진다. 이는 올가미형 고분자 및 수갑형 고분자 체인의 선형 부분이 같은 전단 유동 세기에서 상응하는 선형 고분자 체인(L16)보다 평균적으로 더 늘어나 있다는 것을 의미한다. 특히, 수갑형 고분자 체인의 선형 부분은 올가미형 고분자 체인의 선형 부분보다 같은 전단 유동 세기에서 높은 값을 보여준다.
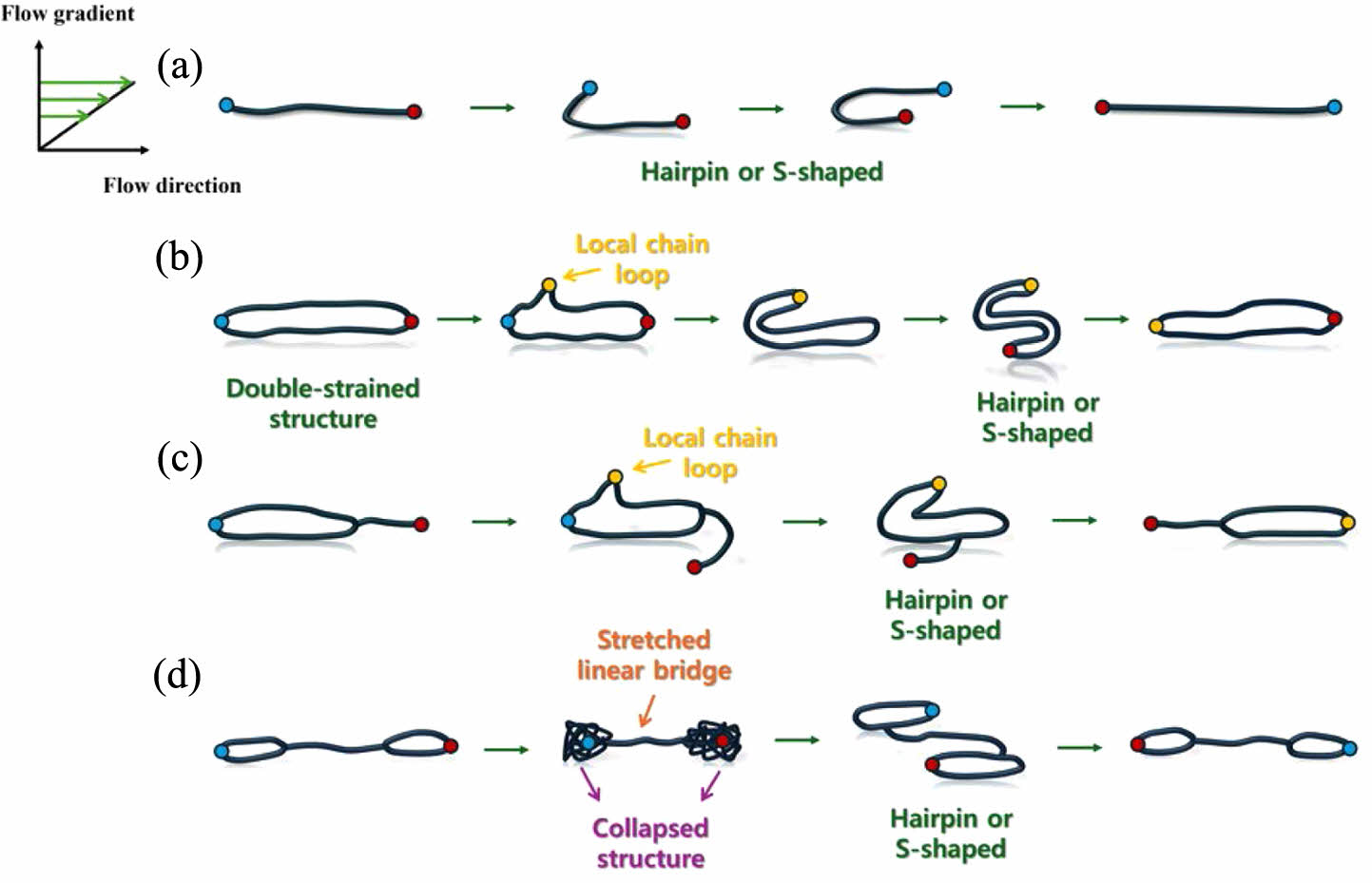
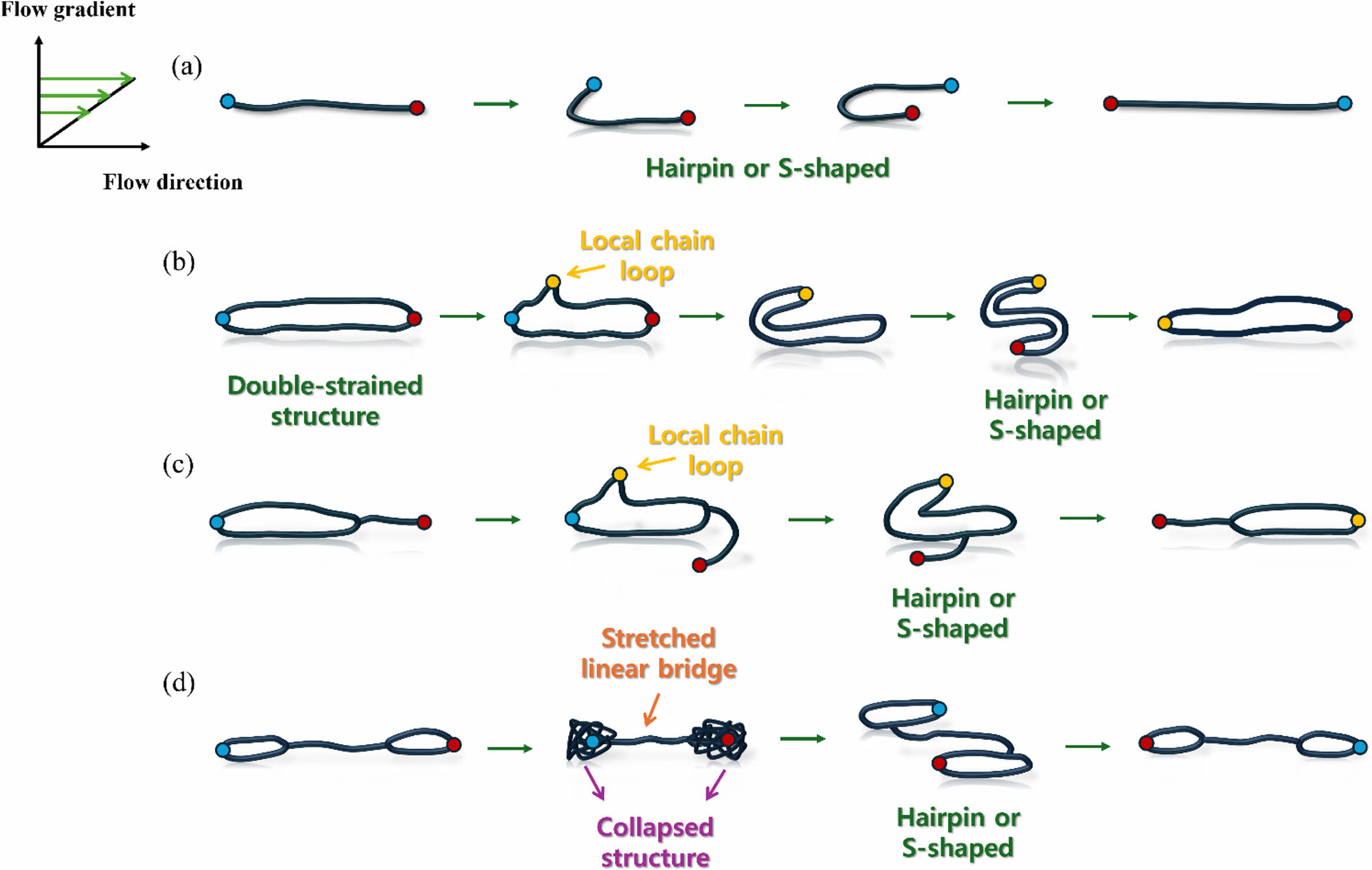
빠른 전단 유동 하에서 각 고분자 체인은 회전 및 텀블링 거동(chain rotation and tumbling behaviour)을 보여준다. Figure 4는 각 고분자 체인의 복잡한 회전 및 텀블링 거동을 간단히 도식화하여 시각적으로 표시하였다. 각 고분자 체인 회전 및 텀블링 거동에 대한 동영상 파일은 부록을 참조하길 바란다. 이전 고분자 용액에 대한 연구 결과와 마찬가지로, Figure 4(a)에서 보듯이, 선형 고분자 체인의 자유 말단(free chain end)이 랜덤하게 움직이다 전단 속도 기울기 차이에 의해 체인 회전 및 텀블링이 시작되게 되는 고분자 체인의 메인 윤곽선(main chain contour)을 따라 움직이므로 헤어핀(hairpin) 또는 S자 모양(S-shaped)으로 회전 및 텀블링 하게 된다.^45-47 자유 배수 용액 하 고리형 고분자 체인은 분자간 또는 분자내 상화 작용(inter- or intra-molecular interactions)이 없기 때문에 빠른 전단 세기에서 고리형 체인의 각 사이드가 서로 접근하여 이중 가닥으로 이루어진 선형 체인 구조(double-stranded linear chain structure)를 만든다. 이중 가닥 구조를 형성한 고리형 고분자의 경우 회전 및 텀블링은 자유 말단(free chain ends) 대신에 속도구배(velocity gradient) 방향으로 올라오는 체인 로컬 루프(chain local loop)로부터 시작되게 된다. 단일 가닥 선형 고분자 체인(single stranded linear polymer chain)과 마찬가지로 이중 가닥 구조의 체인 로컬 루프는 고리형 고분자 체인의 중심 윤곽선을 따라 이동하게 되므로 전체적으로 헤어핀 또는 S자 모양의 회전 및 텀블링을 관찰할 수 있다.
올가미형 고분자 체인의 경우 고리형 부분의 비율이 선형 곁가지 부분의 비율보다 크다. 따라서, 올가미형 고분자 체인은 이중 가닥 구조를 형성하는 순수 고리형 고분자와 비슷한 모습으로 회전 및 텀블링을 하게 된다. Figure 4(c)에서 보듯이, 선형 곁가지 부분의 국소적인 흔들림(local wagging motion)을 제외한다면 올가미형 고분자 체인은 크게 헤어핀 및 S자 모양으로 회전 및 텀블링 하는 것으로 보인다.
Figure 4(d)에서 보듯이, 수갑형 고분자 체인의 경우도 선형 고분자 체인의 회전 및 텀블링 모습과 전체적으로 비슷한 것으로 보인다. 하지만, 수갑형 고분자 체인의 경우 자유 체인 끝 대신에 고리형 부분이 위치하고 있어 선형 고분자 체인의 회전 및 텀블링 거동과는 부분적으로 다른 모습을 보인다. 수갑형 고분자 체인의 경우, 고리형 고분자 체인과 같이 고리형 부분의 체인 로컬 루프가 속도 구배 방향으로 올라가게 되어 회전 및 텀블링 시작된다. 이때, 수갑형 고분자 체인의 선형 브릿지 부분 때문에 선형 고분자 체인처럼 바로 회전 및 텀블링 하는 것이 아니라 고리형 부분은 수축되고 선형 브릿지 부분은 인장되며 헤어핀 또는 S자 모양 텀블링이 시작되게 된다.
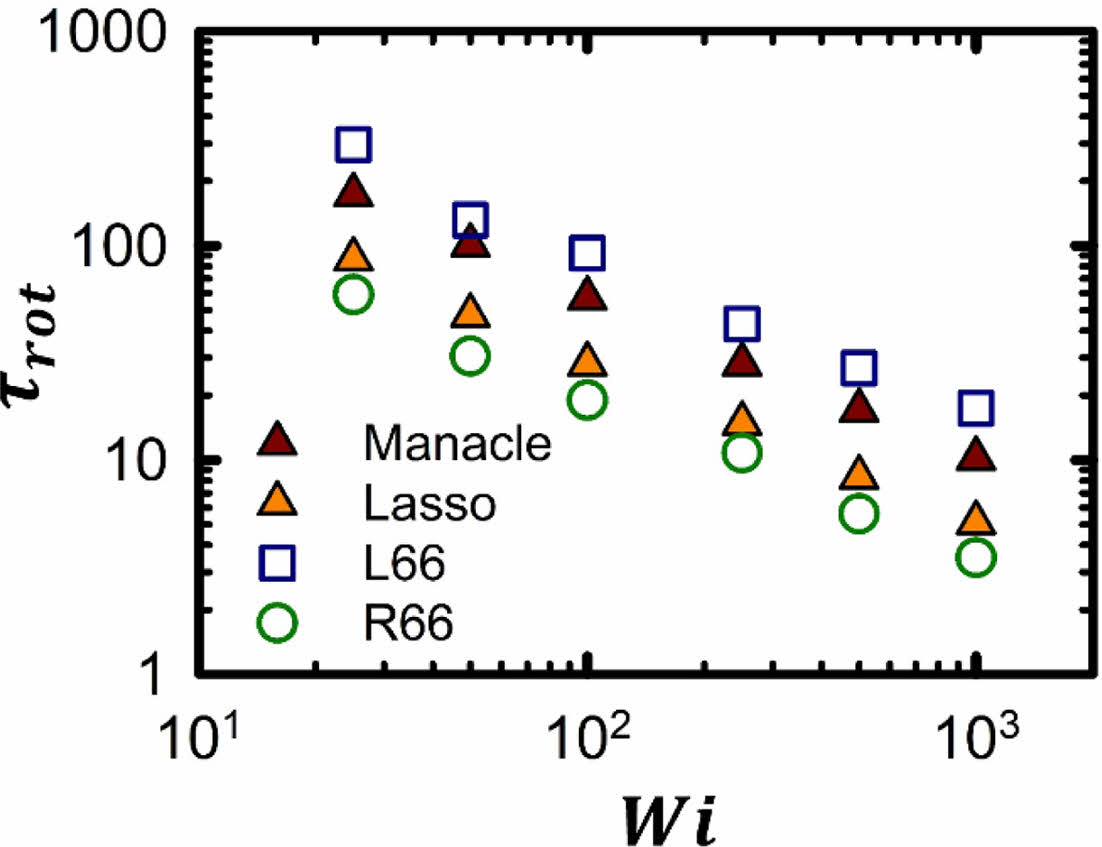
Figure 5에서는 각 고분자 시스템의 체인 회전 시간(chain rotational time)을 전단 유동 세기에 따라 보여주었다. 일반적으로 고리형 고분자 체인은 같은 전단 유동 세기에서 동일한 분자량을 가지는 선형 고분자 체인보다 빠른 회전 시간을 가진다.^20,21 본 연구에서도 자유 배수 용액 하 고리형 고분자 체인(R66)은 같은 전단 유동 세기에서 선형 고분자 체인(L66)보다 빠른 체인 회전 시간을 보여준다. 고리형 부분의 비율이 큰 올가미형 고분자 체인의 경우 같은 전단 유동 세기에서 순수 고리형 고분자 체인(R66)과 비슷한 체인 회전 시간을 보여 주었다. 반면에 선형 브릿지 부분의 역할이 큰 수갑형 고분자 체인의 경우는 같은 전단 유동 세기에서 순수 선형 고분자 체인(L66)과 비슷한 체인 회전 시간을 보여 주었다. 이러한 결과는 앞서 설명한 각 고분자 체인의 회전 및 텀블링 메커니즘과 일맥상통한다. 동일한 전단 유동 세기에서 체인의 회전 시간은 고리형 고분자(R66) < 올챙이형 고분자 < 수갑형 고분자 < 선형 고분자(L66) 순으로 증가한다.
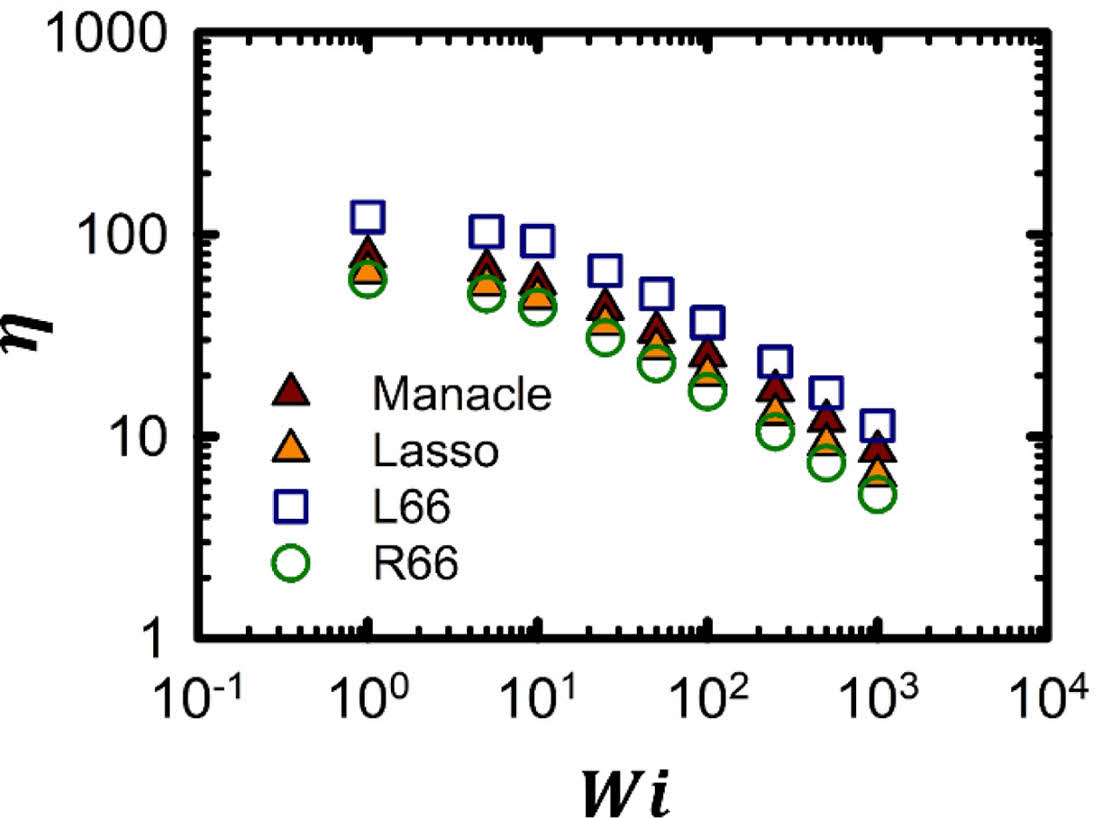
고분자 체인 시스템의 유체역학적 구조 변화와 그에 따른 유변학적 특성을 살펴보기 위해 Figure 6에서 전단 유동 세기에 따른 각 고분자 체인의 점도(viscosity, η) 변화를 관찰해 보았다. 모든 고분자 체인 시스템은 전단 유동 세기가 증가함에 따라 점도가 감소하는 전형적인 면찰 담화(shear thinning) 현상을 보여준다. 각 고분자 체인 시스템의 면찰 담화 정도(degree of shear thinning)는 거듭 제곱 법칙(power-law, h~MW^-b)의 지수(b)로써 측정할 수 있다.¹⁰ 각 고분자 체인 시스템에 대하여 선형 고분자 체인(L66)의 지수는 0.73, 고리형 고분자 체인(R66)의 지수는 0.73, 올가미형 고분자 체인의 지수는 0.72, 수갑형 고분자 체인의 지수는 0.76으로 계산되었다.
고분자 이론 및 실험 결과에 따르면 분자량이 증가함에 따라 고분자의 점도는 증가한다.^9,10,13-15 하지만, 고리형 고분자의 경우 동일한 분자량을 가지는 선형 고분자보다 낮은 점도를 가진다고 알려져 있다.^19-21 같은 전단 유동 세기에서 점도를 비교해 보면, 이러한 사실을 잘 확인할 수 있다. 동일한 전단 유동 세기에서 고리형 고분자(R66)는 선형 고분자(L66)보다 낮은 점도를 가지고 있고, 점도는 고리형 고분자(R66) < 올가미형 고분자 < 수갑형 고분자 < 선형 고분자(L66) 순으로 증가한다. 올가미형 고분자 체인의 경우 고리형 부분이 선형 부분보다 구조적으로나 동역학적으로 큰 역할을 하기 때문에 고리형 고분자와 비슷한 점도를 가질 것으로 예상된다. 수갑형 고분자의 고리형 부분은 선형 고분자의 자유 양쪽 끝과 비슷한 역할을 하며 전체적으로 선형 고분자 체인과 비슷하게 행동하기 때문에 선형 고분자와 비슷한 점도를 가질 것으로 생각된다.
올가미형 고분자 체인과 수갑형 고분자 체인을 비교해 보면 고리형 부분 및 선형 부분에 속해 있는 비드의 수는 각각 50개와 16개로 같지만 체인 내에서 구조와 위치에 따라 역할이 매우 달라지는 것을 볼 수 있다. 올가미형 고분자 체인의 선형 부분은 고리형 부분에 붙어있는 곁가지 정도의 역할을 하고 있으며 체인의 구조적, 동역학적, 유변학적 특성에 큰 영향을 미치지 못하는 것 같다. 올가미형 고분자 체인의 구조적, 동역학적, 유변학적 특성은 체인 내 비율이 큰 고리형 부분의 유체역학적 응답에 기인하는 것 같다. 반면에 수갑형 고분자 체인의 경우는 체인 양쪽에 위치한 고리형 부분에 의해 구조적, 동역학적, 유변학적 특성이 결정되는 것 같다. 양쪽 고리형 부분에서 시작되는 체인 로컬 루프에 의해 고리형 부분이 수축되고 이는 덤벨 모양 고분자 체인(dumbbell-shaped polymer chain)처럼 선형 브릿지 부분을 스트레칭 시킨다. 이로 인해 수갑형 고분자 체인은 선형 고분자 체인처럼 행동하는 것으로 생각된다.

고분자의 체인의 분자 구조는 고분자의 구조적, 동역학적, 유변학적 특성에 많은 영향을 미친다. 본 연구에서는 비드-로드 체인 모델을 채용한 중시 기반 브라운 동역학 전산 모사를 이용하여 선형 및 고리형 부분을 포함하고 있는 고분자 체인의 분자 구조가 고분자 시스템의 구조적, 동역학적, 유변학적 거동에 어떤 영향을 미치는 지를 면밀히 조사해 보았다. 이를 위해 먼저, 동일한 분자량을 지닌 선형(16개 비드) 및 고리형 부분(50개 비드)을 고분자 체인 내에서 조합하여 간단한 올가미형 고분자 체인과 수갑형 고분자 체인 구조를 고안하였다. 이에 상응하는 선형(L66) 및 고리형(R66) 고분자 체인과의 비교 및 분석을 통해 이러한 고분자 체인들의 특성을 이해하고자 하였다.
평형 상태에서 선형, 고리형, 올가미형 그리고 수갑형 고분자 체인들은 랜덤하게 코일된 체인 형태를 보여주었는데 그 크기가 서로 달랐다. 동일한 분자량을 가지는 네 가지 고분자 시스템은 고리형 고분자(R66) < 올가미형 고분자 < 수갑형 고분자 < 선형 고분자(L66) 순으로 체인의 크기가 증가하였다.
고분자 체인의 동적 특성에 큰 영향을 미치는 가장 긴 완화 시간은 분자량의 제곱에 비례하여 증가하는 것으로 알려져 있다. 하지만, 동일한 분자량을 가진 네 가지 고분자 시스템들은 고리형 고분자(R66) < 올가미형 고분자 < 수갑형 고분자 < 선형 고분자(L66) 순으로 완화 시간이 증가하였다.
고분자 체인의 분자 구조에 따른 유체역학적인 형태 변화를 관찰하기 위해 전단 유동 하에서 각 고분자 시스템의 여러 가지 특성들을 관찰하였다. 같은 전단 유동 세기에서 각 고분자 체인 시스템의 크기는 고리형 고분자(R66) < 올가미형 고분자 < 수갑형 고분자 < 선형 고분자(L66) 순으로 증가함을 확인할 수 있었다. 특히, 올가미형 고분자보다 수갑형 고분자의 크기가 증가하는 이유는 양쪽의 고리형 부분으로 인한 중간 선형 브릿지 부분의 스트레칭 때문인 것으로 생각된다.
빠른 전단 유동 하에서 고분자 체인들은 회전 및 텀블링 거동을 하게 된다. 선형 고분자 체인은 자유 체인 끝에서 시작되는 전형적인 헤어핀 및 S자 모양 회전 및 텀블링 거동을 보여준다. 고리형 고분자 체인의 경우는 빠른 전단 유동에 의해 이중 가닥으로 이루어진 선형 체인 구조를 형성하게 된다. 이러한 구조로 인해 고리형 고분자 체인도 자유 체인 끝 대신에 체인 로컬 루프에서 시작되는 헤어핀 또는 S자 모양 회전 및 텀블링 거동을 보여준다. 올가미형 고분자 체인은 선형 곁가지 부분에 비해 고리형 부분의 비율이 크다. 따라서 올가미형 고분자 체인은 순수 고리형 체인과 비슷한 모습으로 헤어핀 또는 S자 모양 회전 및 텀블링 하게 된다. 올가미형 고분자 체인의 선형 곁가지 부분은 회전 및 텀블링 하는 동안 국소적인 흔들림(local wagging)을 보여준다. 수갑형 고분자 체인의 회전 및 텀블링 거동은 전체적으로 선형 고분자 체인의 헤어핀 및 S자 모양 회전 및 텀블링과 비슷하다고 볼 수 있다. 하지만, 수갑형 고분자 체인의 경우 자유 체인 끝을 가지고 있지 않다. 따라서 속도 구배 방향으로 올라간 양쪽 고리형 부분의 체인 로컬 루프로 인해 회전 및 텀블링이 시작된다. 속도 구배 방향으로 올라간 양쪽 고리형 부분은 각각 수축된 상태를 보여주며 선형 브릿지 부분을 스트레칭 시키게 된다. 각 고분자 체인에 대한 이러한 특징적인 회전 및 텀블링 메커니즘들은 각 고분자 체인에 대한 회전 시간 차이를 잘 설명해 줄 수 있다.
고분자 이론 및 실험 결과에 따르면 고분자의 점도는 분자량이 증가함에 따라 증가한다. 하지만, 동일한 분자량을 지니고 있는 네 가지 고분자 시스템을 비교해 보면 점도는 고리형 고분자(R66) < 올가미형 고분자 < 수갑형 고분자 < 선형 고분자(L66) 순으로 증가한다는 사실을 확인할 수 있다. 이러한 결과는 고분자 체인 내에서 선형 부분과 고리형 부분이 어떠한 역할을 하고 있는지에 따라 결정되는 것 같다. 예를 들어, 올가미형 고분자 체인에서 고리형 부분이 큰 비율을 차지하고 있기 때문에 구조적으로나 동역학적으로 주요 역할을 하고 선형 곁가지 부분은 국소적인 역할을 한다. 따라서 올가미형 고분자 체인은 순수 고리형 체인과 비슷한 점도를 가질 것으로 예상된다.
올가미 형태와 수갑형 형태 고분자들은 생체 단백질 분자에서 유사한 구조를 쉽게 찾을 수 있고, 다양한 약물 전달 시스템, 나노 입자와 같은 고성능 복합재료 등에 널리 활용될 수 있다. 본 연구에서는 이러한 고분자 체인 시스템의 평형 상태와 비평형 상태에서의 구조적, 동역학적, 유변학적 특성에 대해 살펴보고 그 원인을 분석하였다. 이러한 연구 결과는 향후 생체 단백질 분자의 이해와, 약물 전달 시스템의 개선 등 바이오 분야에서 매우 유용하게 활용될 것으로 예상되며 기존 고분자 재료의 특성을 개선하거나 새로운 고분자 재료를 개발하는 등의 고성능 복합재료 개발에 적극적으로 활용될 것이라 기대한다.